Robust least squares projection twin SVM and its sparse solution

doi:10.23919/JSEE.2023.000103

Journal of Systems Engineering and Electronics ›› 2023, Vol. 34 ›› Issue (4): 827-838.doi: 10.23919/JSEE.2023.000103

• • 上一篇

收稿日期:2022-04-13 接受日期:2023-06-15 出版日期:2023-08-18 发布日期:2023-08-28

Robust least squares projection twin SVM and its sparse solution

Shuisheng ZHOU¹(), Wenmeng ZHANG¹(), Li CHEN²^,³^,*(), Mingliang XU³()

¹ School of Mathematics and Statistics, Xidian University, Xi’an 710126, China
² School of Physical Education, Zhengzhou University, Zhengzhou 450001, China
³ School of Computer and Artificial Intelligence, Zhengzhou University, Zhengzhou 450001, China

Received:2022-04-13 Accepted:2023-06-15 Online:2023-08-18 Published:2023-08-28
Contact: Li CHEN E-mail:sszhou@mail.xidian.edu.cn;3137710140@qq.com;cli@zzu.edu.cn;iexumingliang@zzu.edu.cn
About author:
ZHOU Shuisheng was born in 1972. He received his M.S. degree in applied mathematics and Ph.D. degree in computer science from Xidian University, Xi ’an, China, in 1998 and 2005, respectively. He is currently a professor in the School of Mathematics and Statistics, Xidian University. His current research interests include optimization algorithm and its application, machine learning, pattern recognition, kernel-based learning, and support vector machines. E-mail: sszhou@mail.xidian.edu.cn

ZHANG Wenmeng was born in 1996. She received her degree in the School of Mathematics and Statistics, Xidian University. Her current research interests include optimization algorithm and its application, machine learning, pattern recognition, kernel-based learning, and support vector machines. E-mail: 3137710140@qq.com

CHEN Li was born in 1982. She received her Ph.D. degree in School of Mathematics and Statistics, Xidian University, Xi ’an, China and M.S. degree in mathematics from China Agricultural University, Beijing, China, in 2019 and 2009, respectively. She is currently an associate professor in Zhengzhou University. Her current research interests include optimization algorithm and its application, machine learning, pattern recognition, and support vector machines. E-mail: cli@zzu.edu.cn

XU Mingliang was born in 1981. He received his Ph.D. degree from the State Key Lab of Computer Aided Design and Computer Graphics, Zhejiang University, China. He is a professor in the School of Computer and Artificial Intelligence, Zhengzhou University, China. His current research interests include computer graphics, multimedia and artificial intelligence. E-mail: iexumingliang@zzu.edu.cn
Supported by:
This work was supported by the National Natural Science Foundation of China (61772020;62202433;62172371;62272422;62036010), the Natural Science Foundation of Henan Province (22100002), and the Postdoctoral Research Grant in Henan Province (202103111)

摘要/Abstract

Abstract:

Least squares projection twin support vector machine (LSPTSVM) has faster computing speed than classical least squares support vector machine (LSSVM). However, LSPTSVM is sensitive to outliers and its solution lacks sparsity. Therefore, it is difficult for LSPTSVM to process large-scale datasets with outliers. In this paper, we propose a robust LSPTSVM model (called R-LSPTSVM) by applying truncated least squares loss function. The robustness of R-LSPTSVM is proved from a weighted perspective. Furthermore, we obtain the sparse solution of R-LSPTSVM by using the pivoting Cholesky factorization method in primal space. Finally, the sparse R-LSPTSVM algorithm (SR-LSPTSVM) is proposed. Experimental results show that SR-LSPTSVM is insensitive to outliers and can deal with large-scale datasets fastly.

Key words: outliers, robust least squares projection twin support vector machine (R-LSPTSVM), low-rank approximation, sparse solution

. [J]. Journal of Systems Engineering and Electronics, 2023, 34(4): 827-838.

Shuisheng ZHOU, Wenmeng ZHANG, Li CHEN, Mingliang XU. Robust least squares projection twin SVM and its sparse solution[J]. Journal of Systems Engineering and Electronics, 2023, 34(4): 827-838.

图/表 6

Data	Algorithm	0% outliers			10% outliers
Data	Algorithm	nSVs	Time/s	Accuracy/%	nSVs	Time/s	Accuracy/%
Hepatitis m = 124 l = 31 n = 19	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	95(0) 124(0) 22.6(19.9) 2.4(2.6) 62(56.8) 4.8(2.7)	0.02(0.01) 0.02(0.01) 0.07(0.01) 0.00(0.00) 0.03(0.01) 0.00(0.00)	90.32(0) 89.25(0.03) 86.45(0.04) 90.32(0) 90.32(0) 90.32(0)	69.7(14.5) 124(0) 26.7(42.7) 4.8(2.7) 82(32.1) 1.3(1.8)	0.03(0.01) 0.01(0.01) 0.07(0.01) 0.00(0.00) 0.03(0.03) 0.01(0.02)	85.81(0.04) 89.03(0.03) 80.64(0.09) 89.03(0.02) 90.32(0.04) 90.97(0.01)
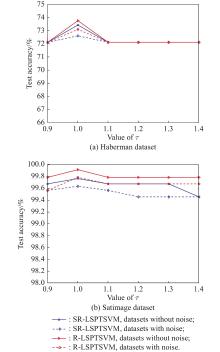
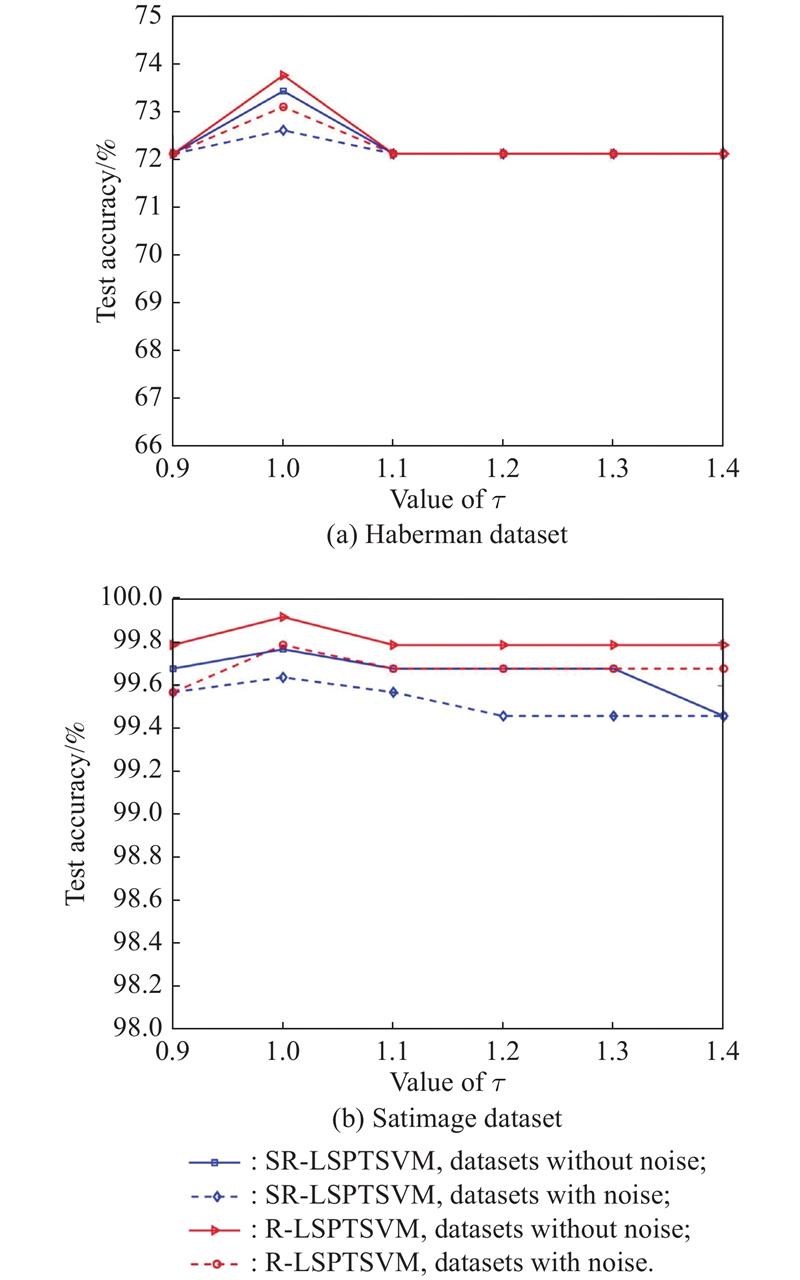
Haberman m = 245 l = 61 n = 3	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	173.2(11.6) 245(0) 35(5.5) 7.2(6.6) 166.6(28.6) 10(0)	0.05(0.02) 0.02(0.01) 0.18(0.08) 0.01(0.00) 0.11(0.01) 0.01(0.00)	70.82(0.02) 71.80(0.02) 70.82(0.03) 72.13(0) 73.77(0) 73.44(0.01)	162.5(8.4) 245(0) 72.6(21.0) 8.6(5.0) 89.1(79.0) 4.3(3.1)	0.04(0.02) 0.02(0.01) 0.17(0.07) 0.00(0.00) 0.03(0.03) 0.01(0.00)	70.00(0.02) 71.47(0.04) 70.00(0.02) 72.13(0) 73.11(0.02) 72.62(0.01)
Breast m = 547 l = 136 n = 10	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	123.2(86.4) 547(0) 62(0) 27(0) 197(0) 8(0)	0.10(0.01) 0.22(0.00) 0.64(0.05) 0.01(0.00) 0.07(0.00) 0.01(0.00)	97.06(0.01) 97.79(0.01) 98.53(0) 98.53(0) 98.53(0) 97.79(0)	269.7(67.4) 547(0) 3.6(4.8) 27(0) 226.5(129.0) 21.7(8.6)	0.10(0.01) 0.23(0.10) 0.64(0.56) 0.00(0.00) 0.16(0.09) 0.01(0.02)	94.19(0.01) 97.50(0.01) 97.94(0.01) 97.20(0.01) 98.53(0.01) 97.72(0.00)
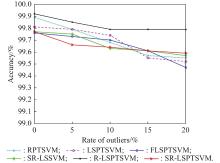
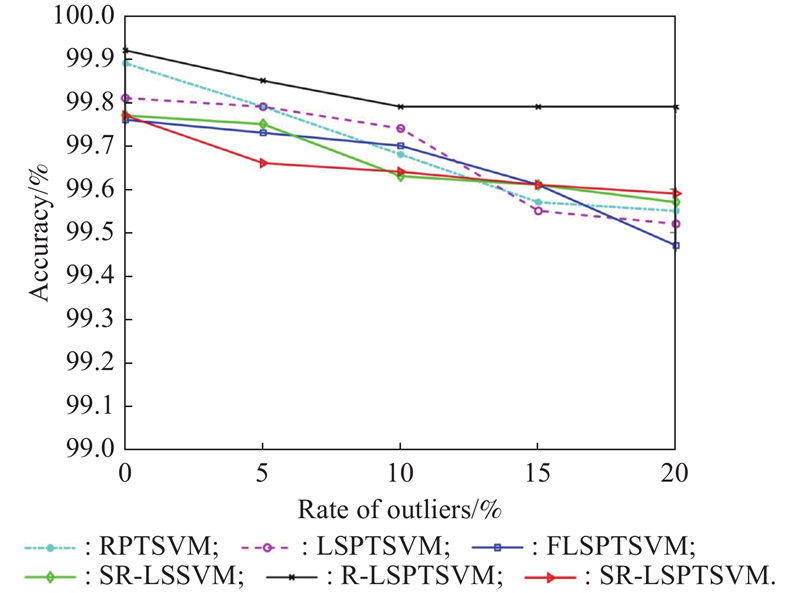
Satimage m = 2110 l = 931 n = 36	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	47.4(5.0) 2110(0) 59.4(54.3) 105(0) 1073.4(54.3) 105(0)	3.60(0.11) 0.98 (0.06) 20.43(1.75) 0.06(0.01) 1.23(0.05) 0.07(0.00)	99.89(0) 99.81(0.00) 99.76(0.00) 99.77(0.00) 99.92(0.00) 99.77(0.00)	1053.8(164.0) 2110(0) 115.4(201.1) 105(0) 1887.6(664.6) 111(11.3)	3.03(1.30) 1.10(0.18) 21.37(1.84) 0.14(0.08) 1.67(0.20) 0.08(0.03)	99.68(0.00) 99.74(0.00) 99.70(0.00) 99.63(0.00) 99.79(0.00) 99.64(0.00)
USPS m = 2199 l = 623 n = 256	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	14(0) 2199(0) 59.5(16.3) 109(0) 1044(0) 109(0)	4.06(0.84) 3.17(0.60) 26.79(0.05) 1.01(0.03) 11.47(0.22) 0.84(0.10)	99.36(0) 99.52(0) 99.44(0.00) 99.52(0) 99.36(0) 99.20(0)	681.9(208.6) 2199(0) 34.4(51.4) 109(0) 907.7(1130.2) 65.2(35.8)	4.25(0.89) 3.52(0.75) 20.43(0.40) 0.48(0.06) 2.08(1.64) 0.33(0.03)	98.65(0.01) 98.74(0.01) 98.62(0.01) 99.12(0.00) 98.65(0.00) 99.15(0.01)
Shuttle m = 9206 l = 2964 n = 9	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	1219(1707.0) 9206(0) 152.4(65.2) 50.2(5.0) 4596(0) 138.2(34.1)	88.65(0.35) 39.25(0.35) 1796.35(0.57) 0.04(0.00) 48.25(1.17) 0.32(0.09)	100(0) 100(0) 99.95(0.00) 99.97(0) 99.93(0) 100(0)	3157.0(2788.0) 9206(0) 182.3(70.4) 126.8(84.3) 4002.3(687.5) 88.2(12.0)	114.67(23.44) 39.39 (0.50) 1821.20(40.05) 0.33 (0.31) 36.42(0.24) 0.09 (0.02)	99.88(0.00) 99.87(0.00) 99.87(0.01) 99.89(0.00) 99.91(0.00) 99.93(0)
Ijcnn1 m = 35000 l = 91701 n = 22	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	— — — 1750(0) — 1750(0)	— — — 28.28(1.10) — 26.78(3.33)	— — — 90.50(0) — 90.50(0)	— — — 1750(0) — 1750(0)	— — — 28.68(1.67) — 26.39(0.23)	— — — 90.50(0) — 90.50(0)
Skin- nonskin m = 61265 l = 183792 n = 3	RPTSVM LSPTSVM FLSPTSVM SR-LSSVM R-LSPTSVM SR-LSPTSVM	— — — 3061(2.31) — 2532.2(21.4)	— — — 128.39(0.86) — 115.23(4.84)	— — — 97.67(0.01) — 98.02(0.00)	— — — 3063(0) — 2661(9.4)	— — — 115.25(0.26) — 114.28(0.60)	— — — 94.49(0.01) — 95.17(0)

参考文献 37

1	CORTES C, VAPNIK V Support-vector networks. Machine Learning, 1995, 20 (3): 273- 297.
2	BURGES C A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery, 1998, 2 (6): 121- 167.
3	OSUNA E, FREUND R, GIROSI F. Training support vector machines: an application to face detection. Proc. of the IEEE Computer Society Conference on Computer Vision & Pattern Recognition, 2000: 130–136.
4	TRAFALIS T B, INCE H. Support vector machine for regression and applications to financial forecasting. Proc. of the IEEE International Joint Conference on Neural Networks, 2000: 348–353.
5	CALISIR D, DOGANTEKIN E A new intelligent hepatitis diagnosis system: PCA-LSSVM. Expert Systems with Applications, 2011, 38 (8): 10705- 10708. doi: 10.1016/j.eswa.2011.01.014
6	ZHANG S J, YANG R, LIU S Y, et al Coupled compressed sensing inspired sparse spatial-spectral LSSVM for hyperspectral image classification. Knowledge-Based Systems, 2015, 79 (5): 80- 89.
7	KHEMCHANDANI R, CHANDRA S Twin support vector machines for pattern classification. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2007, 29 (5): 905- 910. doi: 10.1109/TPAMI.2007.1068
8	KUMAR M A, GOPAL M Application of smoothing technique on twin support vector machines. Pattern Recognition Letters, 2008, 29 (13): 1842- 1848. doi: 10.1016/j.patrec.2008.05.016
9	CHEN X B, YANG J, YE Q L, et al Recursive projection twin support vector machine via within-class variance minimization. Pattern Recognition, 2011, 44 (10/11): 2643- 2655. doi: 10.1016/j.patcog.2011.03.001
10	SHAO Y H, DENG N Y, YANG Z M Least squares recursive projection twin support vector machine for classification. Pattern Recognition, 2012, 45 (6): 2299- 2307. doi: 10.1016/j.patcog.2011.11.028
11	DING S F, HUA X P Recursive least squares projection twin support vector machines for nonlinear classification. Neurocomputing, 2014, 130 (4): 3- 9.
12	SUYKENS J, LUKAS L, VANDEWALLE J. Sparse approximation using least squares support vector machines. Proc. of the IEEE International Symposium on Circuits and Systems, 2002: 757–760.
13	JIAO L C, BO L F, WANG L Fast sparse approximation for least squares support vector machine. IEEE Trans. on Neural Networks, 2007, 18 (3): 685- 697. doi: 10.1109/TNN.2006.889500
14	ZHOU S S Sparse LSSVM in primal using cholesky factorization for large-scale problems. IEEE Trans. on Neural Networks & Learning Systems, 2016, 27 (4): 783- 795.
15	ZHOU S S, LIU M. A new sparse LSSVM method based the revised LARS. Proc. of the IEEE International Conference on Machine Vision & Information Technology, 2017: 46–51.
16	CHENG R J, SONG Y D, CHEN D W, et al Intelligent localization of a high-speed train using LSSVM and the online sparse optimization approach. IEEE Trans. on Intelligent Transportation Systems, 2017, 18 (8): 2071- 2084. doi: 10.1109/TITS.2016.2633344
17	SUN B B, NG W W Y, YEUNG D S Improved sparse LSSVMS based on the localized generalization error model. International Journal of Machine Learning and Cybernetics, 2017, 8 (6): 1853- 1861. doi: 10.1007/s13042-016-0563-6
18	MA Y F, LIANG X, SHENG G, et al Noniterative sparse LS-SVM based on globally representative point selection. IEEE Trans. on Neural Networks and Learning Systems, 2021, 32 (2): 788- 798. doi: 10.1109/TNNLS.2020.2979466
19	SUYKENS J A K, BRABANTER J D, LUKAS L, et al Weighted least squares support vector machines: robustness and sparse approximation. Neurocomputing, 2002, 48 (1): 85- 105.
20	WEI L W, CHEN Z Y, LI J P, et al. Sparse and robust least squares support vector machine: a linear programming formulation. Proc. of the IEEE International Conference on Grey Systems and Intelligent Services, 2007: 1134–1138.
21	WEN W, HAO Z F, YANG X W, et al Robust least squares support vector machine based on recursive outlier elimination. Soft Computing, 2010, 14 (11): 1241- 1251. doi: 10.1007/s00500-009-0535-9
22	YANG X W, TAN L J, HE L F A robust least squares support vector machine for regression and classification with noise. Neurocomputing, 2014, 140 (22): 41- 52.
23	CHEN L, ZHOU S S Sparse algorithm for robust LSSVM in primal space. Neurocomputing, 2018, 275 (1): 2880- 2891.
24	YE Y F, SHAO Y H, DENG N Y, et al Robust L_p-norm least squares support vector regression with feature selection . Applied Mathematics and Computation, 2017, 305 (6): 32- 52.
25	LU X J, LIU W B, ZHOU C, et al Robust least-squares support vector machine with minimization of mean and variance of modeling error. IEEE Trans. on Neural Networks & Learning Systems, 2018, 29 (7): 2909- 2920.
26	ZHOU S S, ZHOU W D Unified SVM algorithm based on LS-DC loss. Machine Learning, 2021, 31 (4): 1- 28.
27	SCHLKOPF B, HERBRICH R, SMOLA A J A generalized representer theorem. Berlin: Springer, 2001.
28	SHALEV-SHWARTZ S, BEN-DAVID S. Understanding machine learning: from theory to algorithms. New York: Cambridge University Press, 2014.
29	YUILLE A L, RANGARAJAN A The concave convex procedure. Neural Computation, 2003, 15 (4): 915- 936. doi: 10.1162/08997660360581958
30	TAO P D, LE T Convex analysis approach to d.c. programming: theory, algorithm and applications. Acta Mathematica Vietnamica, 1997, 22 (1): 289- 355.
31	WANG K N, ZHONG P Robust non-convex least squares loss function for regression with outliers. Knowledge-Based Systems, 2014, 71 (1): 290- 302.
32	ZHOU S S, CUI J T, YE F, et al New smoothing SVM algorithm with tight error bound and efficient reduced techniques. Computational Optimization & Applications, 2013, 56 (3): 599- 617.
33	HE B S, YUAN X M On the O(1/n) convergence rate of the Douglas-Rachford alternating direction method . SIAM Journal on Numerical Analysis, 2012, 50 (2): 700- 709. doi: 10.1137/110836936
34	SHAO Y H, WANG Z, CHEN W J, et al A regularization for the projection twin support vector machine. Knowledge- Based Systems, 2013, 37 (2): 203- 210.
35	GUO J H, YI P, WANG R L, et al Feature selection for least squares projection twin support vector machine. Neurocomputing, 2014, 144 (11): 174- 183.
36	SHAO Y H, ZHANG C H, WANG X B, et al Improvements on twin support vector machines. IEEE Trans. on Neural Networks, 2011, 22 (6): 962- 968. doi: 10.1109/TNN.2011.2130540
37	CHANG C C, LIN C J. LIBSVM: a library for support vector machines. http://www.csie.ntu.edu.tw/~cjlin/libsvm.

Data	Algorithm	nSVs	Time/s	Accuracy/%
Iris m = 120 l = 30 n = 4 k = 3	RPTSVM LSPTSVM FLSPTSVM R-LSPTSVM SR-LSPTSVM	74.1(4.4) 120(0) 8.8(1.7) 79.1(3.7) 6(0)	0.02(0.00) 0.01(0.00) 0.04(0.00) 0.01(0.01) 0.00(0.00)	93.33(0) 96.33(0.03) 92.33(0.02) 96.34(0.02) 96.33(0.02)
Wine m = 143 l = 35 n = 13 k = 3	RPTSVM LSPTSVM FLSPTSVM R-LSPTSVM SR-LSPTSVM	117.9(3.8) 143(3.0) 33.0(3.5) 119.1(2.8) 18.3(3.1)	0.04(0.00) 0.02(0.00) 0.08(0.00) 0.01(0.00) 0.00(0.00)	100(0) 100(0) 98.86(0.01) 100(0) 100(0)
Vehicle m = 677 l = 169 n = 18 k = 4	RPTSVM LSPTSVM FLSPTSVM R-LSPTSVM SR-LSPTSVM	290.4(10.7) 677(0) 49.8(3.7) 579.5(12.3) 33(0)	0.54(0.06) 0.38(0.01) 1.13(0.04) 0.05(0.00) 0.01(0.01)	82.72(0.02) 77.04(0.02) 70.60(0.02) 83.14(0.01) 73.96(0.00)
Segment m = 1848 l = 462 n = 19 k = 7	RPTSVM LSPTSVM FLSPTSVM R-LSPTSVM SR-LSPTSVM	453.6(9.2) 1848(0) 137.4(3.5) 1828.7(18.0) 91.9(0.3)	2.98(0.05) 10.8(0.16) 3.72(0.08) 0.29(0.01) 0.09(0.00)	94.67(0.01) 95.61(0.00) 95.26(0.00) 96.23(0.01) 93.77(0.00)
Pendigits m = 7494 l = 3498 n = 16 k = 10	RPTSVM LSPTSVM FLSPTSVM R-LSPTSVM SR-LSPTSVM	846.6(24.2) 7494(0) 500.4(2.0) 7342.1(21.2) 374(0)	5.54(0.24) 18.59(5.55) 137.34(4.80) 2.95(0.06) 1.11(0.01)	98.03(0.00) 97.45(0.00) 86.99(0.04) 98.08(0.00) 98.05(0.00)

Robust least squares projection twin SVM and its sparse solution

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 6

参考文献 37

相关文章 0

编辑推荐

Metrics

本文评价