Lanchester equation for cognitive domain using hesitant fuzzy linguistic terms sets

doi:10.23919/JSEE.2022.000062

Journal of Systems Engineering and Electronics ›› 2022, Vol. 33 ›› Issue (3): 674-682.doi: 10.23919/JSEE.2022.000062

收稿日期:2021-03-18 出版日期:2022-06-18 发布日期:2022-06-24

Lanchester equation for cognitive domain using hesitant fuzzy linguistic terms sets

Qi HAN^1,*(), Weimin LI^1,*(), Qiling XU²(), Minrui ZHAO¹(), Runze HUO¹(), Tao ZHANG¹()

¹ Air Defense and Antimissile School, Air Force Engineering University, Xi’an 710051, China
² School of Humanities, Economics and Law , Northwestern Polytechnical University, Xi’an 710051, China

Received:2021-03-18 Online:2022-06-18 Published:2022-06-24
Contact: Qi HAN,Weimin LI E-mail:hqzgfc@163.com;touyinyatkv0883@163.com;xuqiling_nwpuer@163.com;zmr0204@163.com;529316534@qq.com;zhangtaov2016@163.com
About author:|HAN Qi was born in 1996. He received his B.S. degree from Air Force Engineering University in 2018. He is currently pursuing his Ph.D. degree in Air Force Engineering University. His research interests include decision making, fuzzy sets, and artificial intelligence. E-mail: hqzgfc@163.com||LI Weimin was born in 1964. He received his Ph.D. degree from University of Electronic Science and Technology of China in 1992. He currently works as a distinguished professor in Air Force Engineering University of China. His research interests include operational research, optimization algorithms, and fuzzy decision making theory. E-mail: touyinyatkv0883@163.com||XU Qiling was born in 1998. She received her B.S. degree from Northwestern Polytechnical University in 2020. Her research interests include Lanchester equation, international finance, derivative securities, asset pricing, and risk management. E-mail: xuqiling_nwpuer@163.com||ZHAO Minrui was born in 1996. He received his B.S. and M.S. degrees from Air Force Engineering University, China in 2018 and 2020 respectively. He is currently pursuing his Ph.D. degree in the Air Force Engineering University. His research interests include machine learning, intelligent algorithms, human-computer interaction, and command-control. E-mail: zmr0204@163.com||HUO Runze was born in 1997. He received his management degree from Southwest University in 2020. He is currently studying for his M.S. degree at Air Force Engineering University. His research interests include command and control, decision optimization and intelligent learning. E-mail: 529316534@qq.com||ZHANG Tao was born in 1992. He received his B.S. degree from Northwestern Polytechnical University in 2016 and M.S. degree from Air Force Engineering University in 2018. He is currently a Ph.D. candidate in Air Defense and Antimissile School, Air Force Engineering University. His research interests are Lanchester equation and control theory. E-mail: zhangtaov2016@163.com
Supported by:
This work was supported by the National Natural Science Foundation of China (61703426) and the National Social Science Foundation of China.

摘要/Abstract

Abstract:

Intelligent wars can take place not only in the physical domain and information domain but also in the cognitive domain. The cognitive domain will become the key domain to win in the future intelligent war. A Lanchester equation considering cognitive domain is proposed to fit the development tendency intelligent wars in this paper. One party is considered to obtain the exponential enhancement advantage on combat forces in combat if it can gain an advantage in the cognitive domain over the other party according to the systemic advantage function. The operational effectiveness of the cognitive domain in war is considered to consist of a series of indicators. Hesitant fuzzy sets and linguistic term sets are powerful tools when evaluating indicators, hence the indicators are scored by experts using hesitant fuzzy linguistic terms sets here. A unique hesitant fuzzy hybrid arithmetical averaging operator is used to aggregate the evaluation.

Key words: Lanchester equation, cognitive domain, hesitant fuzzy set, hesitant fuzzy hybrid arithmetical averaging operator

. [J]. Journal of Systems Engineering and Electronics, 2022, 33(3): 674-682.

Qi HAN, Weimin LI, Qiling XU, Minrui ZHAO, Runze HUO, Tao ZHANG. Lanchester equation for cognitive domain using hesitant fuzzy linguistic terms sets[J]. Journal of Systems Engineering and Electronics, 2022, 33(3): 674-682.

图/表 7

参考文献 31

1	MACKAY N, PRICE C, WOOD A J Weight of shell must tell: a Lanchestrian reappraisal of the battle of jutland. History, 2016, 101 (347): 536- 563. doi: 10.1111/1468-229X.12241
2	JOHNSON I R, MACKAY N J Lanchester models and the battle of Britain. Naval Research Logistics, 2011, 58 (3): 210- 222. doi: 10.1002/nav.20328
3	KEANE T Combat modelling with partial differential equations. Applied Mathematical Modelling, 2011, 35 (6): 2723- 2735. doi: 10.1016/j.apm.2010.11.057
4	KIM D, MOON H, PARK D, et al An efficient approximate solution for stochastic Lanchester models. Journal of the Operational Research Society, 2017, 68 (11): 1470- 1481. doi: 10.1057/s41274-016-0163-6
5	KRESS M, CAULKINS J P, FEICHTINGER G, et al Lanchester model for three-way combat. European Journal of Operational Research, 2018, 264 (1): 46- 54. doi: 10.1016/j.ejor.2017.07.026
6	CAO H H, TIAN S P, ZHANG Y Q Lanchester combat model under psychological factor. Fire Control & Command Control, 2018, 43 (3): 58- 62.
7	DEITCHMAN S A Lanchester model of guerrilla war. Operations Research, 1962, 10 (6): 818- 827. doi: 10.1287/opre.10.6.818
8	TANG Q C, LIU G F Information warfare model improvement based on Lanchester’s equation. Journal of Command and Control, 2017, 3 (3): 201- 207.
9	KRESS M Lanchester models for irregular warfare. Mathematics, 2020, 8 (5): 737. doi: 10.3390/math8050737
10	JOHNSON D D P, MACKAY N J Fight the power: Lanches-ter’s laws of combat in human evolution. Evolution and Human Behavior, 2015, 36 (2): 152- 163. doi: 10.1016/j.evolhumbehav.2014.11.001
11	SONG H Q, ZHAO D M, YUAN C Y Network security situation prediction of improved Lanchester equation based on time action factor. Mobile Networks & Applications, 2021, 26 (3): 1008- 1023.
12	KALLONIATIS A C, HOEK K, ZUPARIC M, et al Optimising structure in a networked Lanchester model for fires and manoeuvre in warfare. Journal of the Operational Research Society, 2021, 72 (8): 1863- 1878. doi: 10.1080/01605682.2020.1745701
13	MCCARTNEY M The solution of Lanchester’s equations with inter-battle reinforcement strategies. Physica A-Statistical Mechanics and Its Applications, 2022, 586, 126477. doi: 10.1016/j.physa.2021.126477
14	ATKINSON M P, KRESS M, MACKAY N J Targeting, deployment, and loss-tolerance in Lanchester engagements. Operations Research, 2021, 69 (1): 71- 81. doi: 10.1287/opre.2020.2022
15	COULSON S G Lanchester modelling of intelligence in combat. IMA Journal of Management Mathematics, 2019, 30 (2): 149- 164. doi: 10.1093/imaman/dpx014
16	CLARK B A, WALTON T. Taking back the seas: transforming the U.S. surface fleet for decision-centric warfare.https://csbaonline.org/research/publications/taking-back-the-seas-transforming-the-u.s-surface-fleet-for-decision-centric-warfare/publication/1.
17	TORRA V Hesitant fuzzy sets. International Journal of Intelligent Systems, 2010, 25 (6): 529- 539.
18	FARHADINIA B Information measures for hesitant fuzzy sets and interval-valued hesitant fuzzy sets. Information Sciences, 2013, 240, 129- 144. doi: 10.1016/j.ins.2013.03.034
19	ZADEH L A The concept of a linguistic variable and its application to approximate reasoning−II. Information Sciences, 1975, 8 (4): 301- 357.
20	LIANG D C, XU Z S The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Applied Soft Computing, 2017, 60, 167- 179. doi: 10.1016/j.asoc.2017.06.034
21	RODRIGUEZ R M, MARTINEZ L, HERRERA F Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. on Fuzzy Systems, 2012, 20 (1): 109- 119. doi: 10.1109/TFUZZ.2011.2170076
22	LIAO H C, XU Z S, ZENG X J Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making. Information Sciences, 2014, 271, 125- 142. doi: 10.1016/j.ins.2014.02.125
23	WU Z B, XU J P A consensus model for large-scale group decision making with hesitant fuzzy information and changeable clusters. Information Fusion, 2018, 41, 217- 231. doi: 10.1016/j.inffus.2017.09.011
24	XIA M M, XU Z S Hesitant fuzzy information aggregation in decision making. International Journal of Approximate Reasoning, 2011, 52 (3): 395- 407. doi: 10.1016/j.ijar.2010.09.002
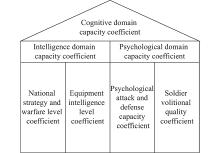
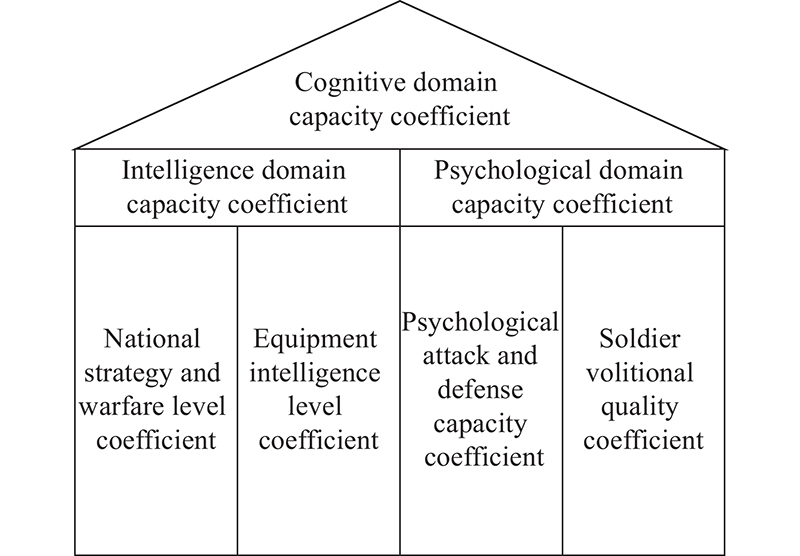
25	LUO Y Y, LI H, WANG R F, et al The characteristics and key technologies of the common domain in the cognitive domain. Defense Technology Review, 2018, 39 (4): 58- 62.
26	WEI C P, RODRIGUEZ R M, MARTINEZ L Uncertainty measures of extended hesitant fuzzy linguistic term sets. IEEE Trans. on Fuzzy Systems, 2018, 26 (3): 1763- 1768. doi: 10.1109/TFUZZ.2017.2724023
27	HU J H, YANG Y, ZHANG X L, et al Similarity and entropy measures for hesitant fuzzy sets. International Transactions in Operational Research, 2018, 25 (3): 857- 886. doi: 10.1111/itor.12477
28	LIAO H C, XU Z S A VIKOR-based method for hesitant fuzzy multi-criteria decision making. Fuzzy Optimization and Decision Making, 2013, 12 (4): 373- 392. doi: 10.1007/s10700-013-9162-0
29	FARHADINIA B Multiple criteria decision-making methods with completely unknown weights in hesitant fuzzy linguistic term setting. Knowledge-Based Systems, 2016, 93, 135- 144. doi: 10.1016/j.knosys.2015.11.008
30	HAN Q, LI W, LU Y L, et al TOPSIS method based on novel entropy and distance measure for linguistic pythagorean fuzzy sets with their application in multiple attribute decision making. IEEE Access, 2020, 8, 14401- 14412. doi: 10.1109/ACCESS.2019.2963261
31	HAN Q, LI Z W, SONG Y F, et al A new method for MAGDM based on improved TOPSIS and a novel Pythagorean fuzzy soft entropy. Symmetry-Basel, 2019, 11 (7): 905. doi: 10.3390/sym11070905

Parameter	${x_1}$	${x_2}$	${x_3}$	${x_4}$
$B$	$\left\{ {{s_5},{s_4}} \right\}$	$\left\{ {{s_5}} \right\}$	$\left\{ {{s_5},{s_4},{s_3}} \right\}$	$\left\{ {{s_6},{s_5}} \right\}$
$R$	$\left\{ {{s_6}} \right\}$	$\left\{ {{s_6},{s_5}} \right\}$	$\left\{ {{s_7},{s_6}} \right\}$	$\left\{ {{s_8},{s_6}} \right\}$

Lanchester equation for cognitive domain using hesitant fuzzy linguistic terms sets

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 7

参考文献 31

相关文章 0

编辑推荐

Metrics

本文评价